On February 28, 2020 Arpit Dua successfully defended his thesis: “Structure of fracton stabilizer models” (Advisor: Meng Cheng/Liang Jiang).
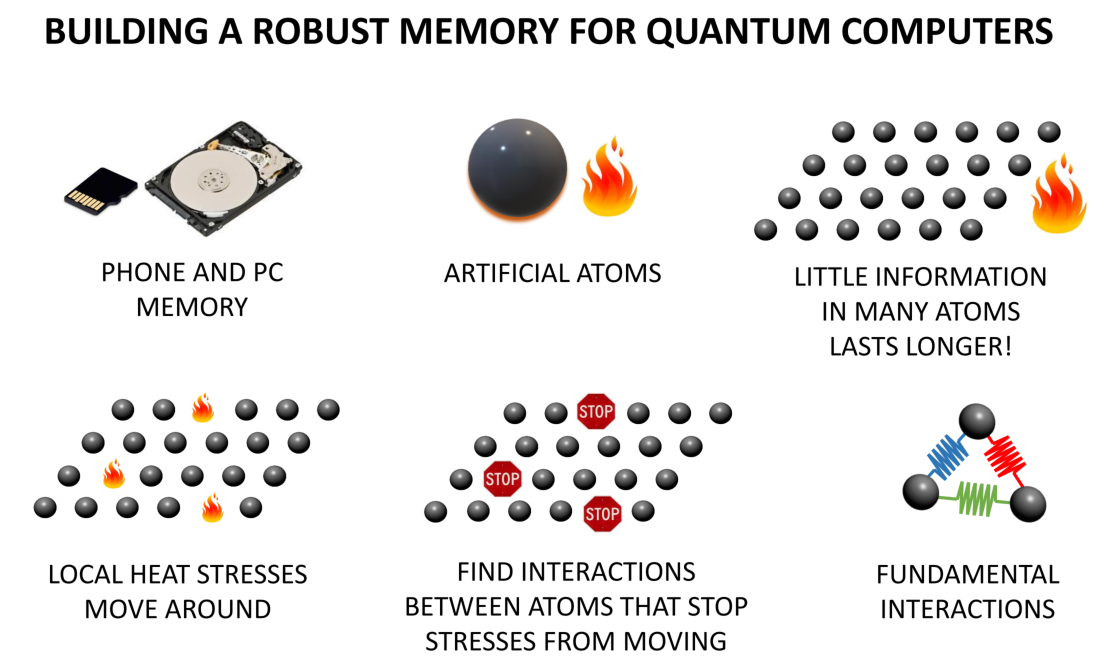
Dua explained “What happens when our minds are stressed out? We have a hard time remembering and analyzing things! Unlike us, the memories of our phones and computers can face immense stress such as heat, or impulsive forces. That’s why when you drop your phone, you worry about its screen and not its memory! My thesis studies how to control stresses on the memory of a new kind of computer called the quantum computer. This computer has a completely novel design and rules of operation that enable it to solve problems that our conventional supercomputers cannot. Solving such problems will lead to advancements in many fields such as drug design, nanotechnology and data encryption. But because of its novelty of operation, conventional memory designs do not work. Unlike your computer which use currents to store information, the smallest units of information in a quantum computer are formed by artificial atoms made in labs. These atoms are sensitive to environmental stresses, predominantly heat and thus, the information stored in them is vulnerable. A crude way to make the memory of a quantum computer robust is to store only a small amount of information redundantly in many atoms and remove local heat stresses actively. Over time though, these stresses propagate to many atoms and the memory is eventually corrupted. Researchers have designed various interactions between atoms to restrict the stresses from moving around. Imagine these interactions as insulating springs connecting atoms- springs that don’t conduct heat. In the lab, such interactions can be made by shining light on the atoms in a unique fashion. Until now such interactions have been found via a hit and miss approach. My work shows that just like each visible color is made from fundamental colors red, green and blue, stress reducing interactions between atoms can be made from only a few fundamental interactions. Knowing these fundamental interactions simplifies the design process immensely. We can now hope to find interactions which don’t allow stresses to be created at all, as if each atom has its own shower to cool down. A memory in which stresses are inherently absent due to its design would be a big steppingstone towards a working quantum computer.”
Dua will join Caltech as a UQM-IQIM Postdoctoral Scholar.
Thesis abstract: “In recent years the study of topological phases of matter has moved to the forefront of theoretical condensed matter physics. This has been fueled in part by the theorized existence of exotic phases of matter that can serve as topological quantum memories and computers. The classification of topological phases of matter in two spatial dimensions in terms of anyon theories, or modular tensor categories, and chiral central charges forms the cornerstone of the subject. For the special case of 2D translation invariant topological stabilizer models this classification was established rigorously at the level of lattice Hamiltonians. In three spatial dimensions, recent steps have been taken towards a similar goal, with some success for topological phases that admit a topological quantum field theory (TQFT) description. However, the burgeoning field of fracton topological phases present a new and challenging facet of the classification problem, as practically all the familiar tools from the study of TQFTs no longer apply.